PERSAMAAN KUADRAT

PERSAMAAN KUADRAT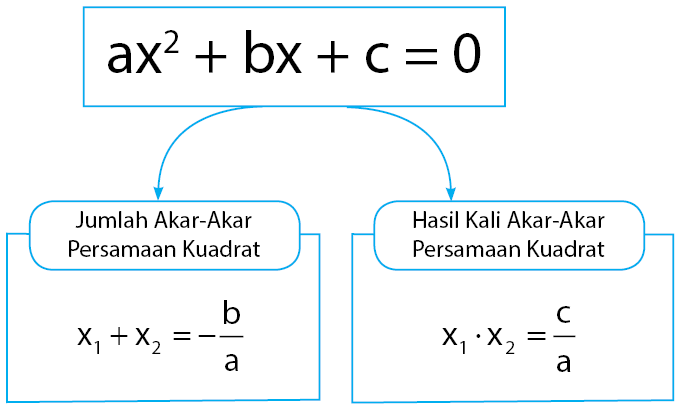

1. Pengertian Persamaan Kuadrat

Persamaan kuadrat adalah suatu persamaan yang pangkat tertinggi dari variabelnya adalah 2.
Bentuk umum persamaan kuadrat:

ax2 + bx + c = 0, a≠0 dan a,b,c elemen R

Dengan: 

x adalah variabel dari persamaan kuadrat 

a adalah koefisien x2

b adalah koefisien x

c adalah konstanta

2. Cara Penyelesaian Persamaan Kuadrat
Ada 3 cara untuk menyelesaikan soal-soal yang berbentuk persamaan kuadrat yakni:
a. Memfaktorkan
    ax2 + bx + c = 0, a≠0 dapat diuraikan menjadi: (x - x1) (x - x2) = 0
b. Menggunakan Rumus Kuadrat (Rumus abc)
    Rumus untuk menentukan akar-akar persamaan kuadrat ax2 + bx + c = 0, a≠0 adalah:

c. Melengkapkan Kuadrat Sempurna
Cara menyelesaikan persamaan kuadrat dengan melengkapkan kuadrat sempurna adalah dengan  mengubah persamaan kuadrat menjadi bentuk kuadrat sempurna. Bentuk umum persamaan kuadrat berbentuk kuadrat sempurna adalah

(x+p)2 = q, dengan q > 0

3.  Menentukan Jenis Akar-akar Persamaan Kuadrat

Jenis akar-akar persamaan kuadrat  ax2 + bx + c = 0 dapat ditentukan oleh nilai diskriminan D = b2 - 4ac 

a. Kedua akar nyata dan berlainan (x1 ≠ x2)  <=> D > 0

b. Kedua akar nyata dan sama (x1 = x2) <=> D = 0

c. Kedua akar tidak nyata (imaginer) <=> D < 0

d. D = k2, dengan k2= bilangan kuadrat sempurna kedua akar rasional

4. Jumlah dan Hasil Kali Akar-akar Persamaan Kuadrat

Untuk menghitung jumlah dan hasil kali akar-akar persamaan kuadrat ax2 + bx + c = 0, dengan a≠0 dapat dicari tanpa terlebih dahulu mencari akar-akarnya.
Dari rumus:

dapat diperoleh:

x1 + x2 =-b/a dan x1.x2 = c/a

Rumus-rumus lain yang dapat digunakan adalah

5. Sifat-Sifat Akar Persamaan Kuadrat
Jika x1 dan x2 adalah akar-akar persamaan kuadrat ax2 + bx + c = 0, a≠0 maka berlaku sifat-sifat berikut ini:

a. Syarat mempunyai dua akar positif

b. Syarat mempunyai dua akar negatif

c. Syarat mempunyai dua akar berlainan tanda

d. Syarat mempunyai dua akar berlawanan

 e. Syarat mempunyai dua akar berkebalikan

Kumpulan Soal Lengkap Menyelesaikan Persamaan Kuadrat

Contoh 1 (SKALU 1978)

Bila x1 dan x2 adalah akar-akar persamaan kuadrat x2 - 6x - 5 = 0, maka x12 + x22 adalah.....

A. 26   

B. 31    
C. 37    
D. 41    
E. 46 

Pembahasan:

Persamaan  x2 - 6x - 5 = 0 memiliki koefisien a =1, b = -6, dan c = -5

x1 + x2= (-b)/a = -(-6)/1 = 6

x1 . x2 = c/a = (-5)/1 = -5

x12 + x22 = (x1 + x2)2 - 2x1.x2

                = (6)2- 2(-5)

                = 36 + 10

                = 46 -------> Jawaban: E

Contoh 2 (PPI 1979)

Bila x1 dan x2 adalah akar-akar persamaan kuadrat x2 - 5x + 9 = 0, maka x13 + x23 sama dengan.....

A. 10    
B. 5    

C. 1    
D. -5    
E. -10

Pembahasan:

Persamaan  x2 - 5x + 9 = 0 memiliki koefisien a =1, b = -5, dan c = 9

x1 + x2= (-b)/a = -(-5)/1 =5

x1 . x2 = c/a = 9/1 = 9

x13 + x23 = (x1 + x2)3 - 3x1.x2(x1 + x2)
                = (5)3-3(9)(5)
                = 125 -135
                = -10  ------------> Jawaban: E

Contoh 3 (SIPENMARU 1988)
Jumlah kebalikan akar-akar persamaan  3x2 - 9x + 4 = 0 adalah.....
A. -4/9    
B. -3/4   
C. -9/4   
D. 9/4    
E. 3/4
Pembahasan:
Persamaan  3x2 - 9x + 4 = 0 memiliki koefisien a =3, b = -9, dan c = 4

x1 + x2= (-b)/a = -(-9)/3 = 3

x1 . x2 = c/a = 4/3
Jumlah kebalikan akar-akarnya adalah
1/x1 + 1/x2 = (x1 + x2) : (x1.x2)
                   = 3: (4/3)
                   = 9/4 -----------> Jawaban: D

Contoh 4 (PPI 1981)
Akar-akar persamaan  2x2 - 6x - p = 0 adalah x1 dan x2. Jika x1 - x2 = 5, maka nilai p adalah.....
A. 8    
B.6    
C.4    
D.-6    
E.-8
Pembahasan:
2x2 - 6x - p = 0 memiliki koefisien a= 2, b = -6 dan c = -p
x1 + x2 = -b/a = -(-6)/2 = 3
x1 + x2 = 3
x1  - x2 = 5
------------- +
<=> 2x1 = 8
<=> x1 = 4
Subtitusi nilai x1 = 4 diperoleh:
x1 + x2 = 3
<=> x2 = 3 - x1
<=> x2 = 3 - 4
<=> x2 = -1
Nilai p :
x1 . x2 =c/a
<=> (4).(-1) = -p/2
<=> -8 = -p
<=> p = 8 --------------> Jawaban: A

Menyelesaikan persamaan kuadrat berdasarkan sifat-sifat akar persamaan kuadrat
Contoh 5 (UMPTN 1993)
(m + 3)x2 + 2(m - 7)x + m-3 = 0 akan mempunyai akar-akar positif jika.....
A. -3< m <3      
B. 3< m < 29/7    
C. -3 < m < 7
D. -7 < m < 3    
E. -29/7 < m < -3
Pembahasan:
Dari  (m + 3)x2 + 2(m - 7)x + m-3 = 0, diperoleh a = m + 3, b = 2(m- 7), dan c = m-3
Syarat mempunyai akar positif:
1) D = b2 - 4ac ≥ 0
  <=> (2(m-7))2 - 4(m+3)(m - 3) ≥ 0
  <=> 4(m2- 14m + 49) - 4(m2 - 9)  ≥ 0
  <=>  m2- 14m + 49 - m2 + 9 ≥ 0
  <=> -14m + 58 ≥ 0
  <=> -14m ≥ -58
  <=> m ≤ 58/14
  <=> m ≤ 29/7
2) x1 + x2 > 0
  <=> -b/a > 0
  <=> -2(m -7)/(m+3) >0
  <=> -3 < m < 7
3) x1.x2 > 0
  <=> c/a > 0
  <=> (m - 3)/(m + 3) > 0
  <=> m < -3 atau m > 3 
(1) ∩ (2) ∩ (3) = 3 < m < 29/7 ---------> Jawaban: B

Menyusun persamaan kuadrat yang telah diketahui akar-akarnya
Contoh 6 (PPI 1980)
Jika 2 dan 3 akar-akar persamaan kuadrat, maka persamaan kuadrat yang dimaksud adalah.....
A. x2 + x + 5 = 0    
B. x2 + 6x + 5 = 0    
C. x2 + 5x - 6 = 0
D. x2 - 5x + 6 = 0    
E. x2 + x + 5 = 0
Pembahasan:
Misalkan x1 = 2 dan x2 = 3, maka:
x1 + x2 = 2 + 3 = 5
x1 . x2 = 2 . 3 = 6
Persamaan kuadrat yang dimaksud adalah
x2- (x1 + x2)x + x1.x2 =0
x2- 5x + 6 = 0 -------------> Jawaban: D

Sumber : ilmuku-duniaku14.blogspot.com