[ MATEMATIKA ] STATISTIKA TUNGGAL DAN DATA KELOMPOK

Rumus Mean, Median, dan Modus Data Kelompok

Pengertian nilai mean, median, dan modus antara data kelompok dan tunggal sama. Nilai mean adalah rata – rata dari data yang diberikan. Nilai median adalah nilai tengah dari data yang telah diurutkan. Sedangkan modus adalah nilai yang paling sering muncul atau nilai dengan frekuensi paling tinggi. Cara mendapatkan nilai mean, median, dan modus pada data tunggal cukup mudah. Ringkasan cara mendapatkan nilai mean, median, dan modus diberikan seperti pada tabel di bawah.

Cara mencari mean, media, modus untuk data kelompok berbeda dengan rumus mean, rumus median, rumus modus data tunggal. Hal ini dikarenakan penyajian data tunggal dan data kelompok juga berbeda.

Sebelumnya, akan dijelaskan dulu tentang bentuk penyajian data kelompok. Pengantar data kelompok menjadi cukup penting karena di dalamnya terdapat istilah dari nilai yang digunakan untuk mencari nilai mean, median, dan modus.

Silahkan Simak Ya Penjelasannya

Penyajian Data Kelompok

Data berkelompok dapat disajikan dalam bentuk tabel distribusi frekuensi, diagram batang, dan lain sebagainya. Agar pembahasan tidak terlalu panjang, akan diambil dua contoh bentuk penyajian data, yaitu data bentuk tabel dan data bentuk diagram batang. Karena, pada dasarnya ide yang digunakan adalah sama.

Sekarang, perhatikan penjelasan tentang data kelompok.

Penyajian data kelompok dalam bentuk tabel.

Di dalam data kelompok berbentuk tabel memuat nilai batas bawah kelas, panjang kelas, dan nilai frekuensi dari kelas terkait.

Penyajian data dalam bentuk diagram batang.

Selanjutnya, simak rumus mean, median, modus data kelompok berikut. Pembahasan pertama adalah rumus mean (rata-rata) data kelompok.

Rumus Mean (Rata-rata) Data Kelompok

Inti dari menentukan nilai rata-rata dari suatu data kelompok sama dengan mencari nilai rata-rata data tunggal. Idenya adalah menjumlahkan semua data kemudian membagi dengan banyaknyanya data. Hanya saja, karena penyajian data kelompok diberikan dalam bentuk berbeda, maka rumus mencari nilai mean untuk data kelompok sedikit berbeda dengan cara mencari nilai mean pada data tunggal.

Keterangan:

$\bar{x}$ = rataan hitung dari data kelompok

fi = frekuensi kelas ke-i

xi = nilai tengah kelas ke-i

Contoh 1: soal dan pembahasan cara mencari nilai median pada data kelompok.

Perhatikan data pada tabel berikut!

Contoh soal mencari mean pada data kelompok

Nilai mean (rata-rata) dari data pada tabel tersebut adalah ….

A. 60,75
B. 61,75
C. 62,75
D. 63,75
E. 64,75

Pembahasan:

Untuk menentukan rata-rata dari suatu kelompok, kita membutuhkan nilai tengah dari masing-masing kelas. Nilai tengah dari masing-masing kelas dapat diperoleh menggunanan rumus berikut.

Nilai tengah masing-masing kelas adalah sebagai berikut.

$x_{1} = \frac{40,5 + 30,5}{2} = \frac{71}{2} = 35,5$

$x_{2} = \frac{50,5 + 40,5}{2} = \frac{91}{2} = 45,5$

$x_{3} = \frac{60,5 + 50,5}{2} = \frac{111}{2} = 55,5$

$x_{4} = \frac{70,5 + 60,5}{2} = \frac{131}{2} = 65,5$

$x_{5} = \frac{80,5 + 70,5}{2} = \frac{151}{2} = 75,5$

$x_{6} = \frac{90,5 + 80,5}{2} = \frac{171}{2} = 85,5$

Hasil perkalian nilai tengah masing-masing kelas dan frekuensinya dapat dilihat pada tabel di bawah.

Sehingga

Jadi, nilai mean dari data yang diberikan pada soal adalah 61,75.

Jawaban: B

Rumus Median Data Kelompok

Median adalah data tengah setelah diurutkan. Pada data tunggal, nilai mediannya dapat diperoleh dengan mengurutkan datanya kemudian mencari data yang terletak di tengah. Hampir sama dengan cara mencari median pada data tunggal, nilai median pada data kelompok juga merupakan nilai tengah dari suatu kumpulan data.

Karena penyajian data disajikan dalam bentuk kelompok, datanya tidak dapat diurutkan seperti pada data tunggal. Oleh karena itu, untuk mencari nilai median data kelompok digunakan sebuah rumus. Rumus median data kelompok adalah sebagai berikut.

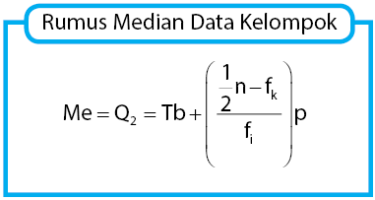
Keterangan:

Tb = tepi bawah kelas median

n = jumlah seluruh frekuensi

fk = jumlah frekuensi sebelum kelas median

fi = frekuensi kelas median

p = panjang kelas interval

Seringkali, data kelompok dibagi menjadi empat bagian yang sama banyak. Pembagian data kelompok menjadi empat sama banyak ini dipisahkan oleh tiga nilai kuartil, yaitu kuartil atas (Q1), kuartil tengah (Q2), dan kuartil bawah (Q3).

Median adalah data ke – n yang membagi banyak data menjadi dua sama banyak. Begitu juga dengan kuartil tengah (Q2). Sehingga, nilai kuartil tengah (Q2) akan sama dengan median.

Contoh 2: soal dan pembahasan cara mencari nilai median pada data kelompok.

Perhatikan data pada tabel berikut!

Nilai median dari data pada tabel tersebut adalah ….

A. 60,32
B. 61,22
C. 61,32
D. 62,22
E. 62,32

Pembahasan:

Jumlah data yang diberikan pada tabel adalah 40. Sehingga letak Median (Q2) berada pada data ke-:

$Q_{2} = \frac{1}{2} \times 40 = 20$

Letak median berada di data ke-20.

Sebelum menentukan nilai mediannya, kita tentukan frekuensi komulatif kurang dari dan letak kelas di mana terdapat data median.

Gunakan tabel yang diberikan pada soal.

Berdasarkan data pada tabel di atas, dapat diperoleh informasi seperti berikut.

Tb = 61 – 0,5 = 60,5

p = 10

fkk = 18

fi = 11

Menghitung nilai median:

$Me = Tb + \left( \frac{\frac{1}{2}n - fkk}{f_{i}} \right) \times p$

$Me = 60,5 + \left( \frac{\frac{1}{2} \cdot 40 - 18}{11} \right) \times 10$

$Me = 60,5 + \left( \frac{20 - 18}{11} \right) \times 10$

$Me = 60,5 + \left( \frac{2}{11} \right) \times 10$

$Me = 60,5 + 1,82 = 62,32$

Jadi, nilai mediannya adalah 62,32.

Jawaban: D

Berikutnya adalah rumus modus data kelompok.

Rumus Modus Data Kelompok

Pengertian modus adalah nilai data yang paling sering muncul atau data yang mempunyai nilai frekuensi paling tinggi. Cara mencari nilai modus pada data tunggal sangat mudah, sobat idschool hanya perlu mencari data dengan frekuensi paling banyak.

Cara mencari nilai modus data kelompok tidak semudah mencari nilai modus pada data tunggal. Hal ini dikarenakan penyajian data kelompok yang disajikan dalam sebuah rentang kelas. Sehingga, nilai modus data kelompok tidak mudah untuk langsung didapat.

Untuk mendapatkan nilai modus data kelompok dapat menggunakan sebuah rumus. Rumus modus data kelompok dapat dilihat seperti persamaan di bawah.

Keterangan:

Tb = tepi bawah kelas modus

d1 = selisih frekuensi kelas modus dengan frekuensi sebelum kelas modus

d2 = selisih frekuensi kelas modus dengan frekuensi setelah kelas modus

p = panjang kelas interval

Contoh 3: soal dan pembahasan modus pada data kelompok.

Perhatikan gambar diagram batang di bawah!

Modus dari data yang disajikan pada diagram batang di atas adalah ….

A. 46,0
B. 46,5
C. 47,0
D. 49,0
E. 49,5

Pembahasan:

Dari diagram diketahui modus ada pada interval 45 – 49, sehingga

$Tb = 45 - 0,5 = 44,5$

$d_{1} = 12 - 8 = 4$

$d_{2} = 12 - 6 = 6$

Maka nilai Modus (Mo) dari data tersebut adalah:

$Mo = Tb + \left( \frac{d_{1}}{d_{1} + d_{2}} \right) \times p$

$Mo = 44,5 + \left( \frac{4}{4 + 6} \right) \times 5$

$Mo = 44,5 + \left( \frac{4}{10} \right) \times 5$

$Mo = 44,5 + 2 = 46,5$

Jawaban: B

Selesai

Sekian pembahasan mengenai rumus mean, median, modus data kelompok. Meliputi rumus mean data kelompok, rumus median data kelompok, dan rumus modus data kelompok. Terimakasih sudah mengunjungi idschool(dot)net, semoga bermanfaat.

Sumber : https://idschool.net

Sebelumnya, akan dijelaskan dulu tentang bentuk penyajian data kelompok. Pengantar data kelompok menjadi cukup penting karena di dalamnya terdapat istilah dari nilai yang digunakan untuk mencari nilai mean, median, dan modus.